

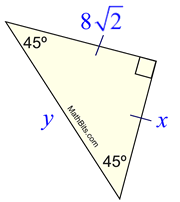
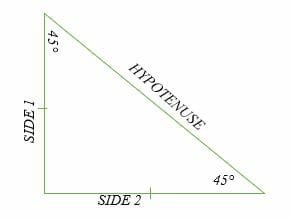
Rather, whatever length is across from 45 degrees, call it a length of x, will be accompanied across from the hypotenuse by a side that is √2 as big, or x√2. The ratio of sides does not mean that the sides opposite the 45 degree angles are necessarily equal to 1, as they are above. The sides in every 45-45-90 triangle have lengths in the ratio 1: 1: √2. If you try setting a = 1, then you get c = √2, as in the diagram above. Is true, but if a = b (because we are talking about an isosceles triangle), we can substitute that into the Pythagorean Theorem to get: If a triangle is a right triangle and it’s isosceles, then the two sides other than the right angle must add up to 90 degrees and they must be equal, so each must equal 45 degrees.įurthermore, since it’s a right triangle, we know that All of the general triangle rules apply to it, the Pythagorean Theorem applies to it, and then it has some special properties of its own.Ī 45-45-90 triangle is what you get when you have an isosceles right triangle. Insofar as a right triangle is a special triangle, the 45-45-90 triangle is doubly special. On the GMAT, you are expected to know the angles and the side relationships for 45-45-90 and 30-60-90 triangles, but you are not expected to have memorized or to be able to determine the angles for Pythagorean triples listed above you can determine the side lengths simply using the Pythagorean formula. You don’t need to know the angles of these triangles, only the ratios of the side lengths: You should memorize at least the first three triples here.
Common Pythagorean TriplesĬertain trios of numbers that satisfy the Pythagorean Theorem appear often on the GMAT. You will then be able to find the length of the third side by plugging the two known lengths intoĮarlier, we’ve discussed how the Pythagorean Theorem can be used to compute the distance between any two points in the coordinate plane.
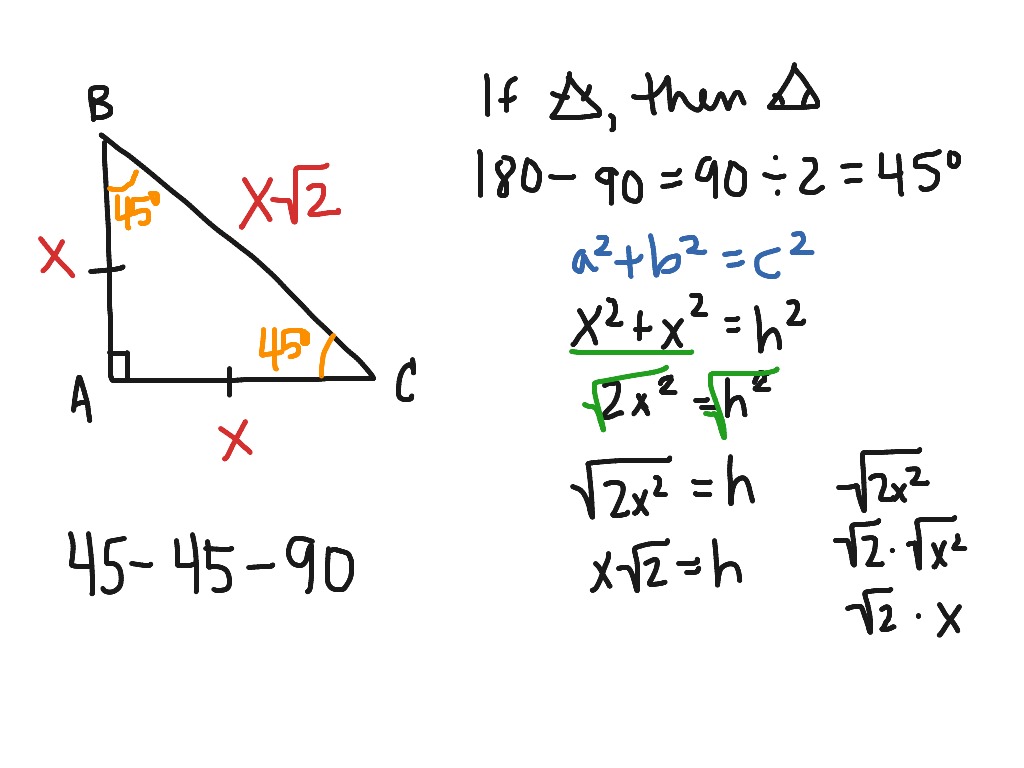
Quite frequently on the GMAT, you will find yourself in a situation in which you know that a particular triangle is a right triangle, and you will know the lengths of two of the three sides. For example, on a typical GMAT question you might use the Pythagorean Theorem to determine the base and height of a triangle and then ultimately find its area. Nevertheless, it’s important to recognize that both formulas refer to the same sides. The sides that we referred to as b and h above are now labeled as b and a, since the custom when using the Pythagorean Theorem is to employ the variables a, b, and c. The Pythagorean Theorem states that, in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. The area of the rectangle is ( b)( h), so either one of the congruent right triangles forming it has an area equal to half of that rectangle. This is intuitively logical because another congruent right triangle can be placed against it so that the hypotenuses are the same line segment, forming a rectangle with sides having length b and width h. If the lengths of both the legs are known, then by setting one of these sides as the base b and the other as the height h, the area of the right triangle is easy to calculate using the standard formula for a triangle’s area:
The legs (or their lengths) are usually labeled a and b.Įither of the legs can be considered a base and the other leg would be considered the height (or altitude), because the right angle automatically makes them perpendicular. When using the Pythagorean Theorem, the hypotenuse or its length is often labeled with a lower case c. The sides adjacent to the right angle are the legs. The side opposite the right angle is called the hypotenuse. Since the three interior angles of a triangle add up to 180 degrees, in a right triangle, since one angle is always 90 degrees, the other two must always add up to 90 degrees (they are complementary). Right triangles are triangles in which one of the interior angles is 90 degrees, a right angle.


 0 kommentar(er)
0 kommentar(er)
